Interfaz de scracht

REGLETAS DE CUSEINAIRE

Regletas de Cuisenaire


Las regletas de Cuisenaire son un versátil juego de manipulación matemática utilizado en la escuela, así como en otros niveles de aprendizaje e incluso con adultos. Se utilizan para enseñar a una amplia variedad de temas matemáticos, como las cuatro operaciones básica, fracciones, área, volumen, raíces cuadradas, resolución de ecuaciones simples, los sistemas de ecuaciones, e incluso ecuaciones cuadráticas.


Aunque se utilizan principalmente para las matemáticas, también se han vuelto populares en el aula de enseñanza de idiomas, en particular, The Silent Way. Pueden ser usadas para enseñar temas como preposiciones de lugar, frases y pronunciación.
Las regletas (réglettes en francés original) fueron llamadas así luego de que su inventor, Georges Cuisenaire (1891-1976), un profesor de escuela primaria de Bélgica, publicara un libro sobre su uso en 1952, llamado Los números en colores. El uso de regletas para la enseñanza tanto de las matemáticas como de idiomas fue desarrollado y popularizado por Caleb Gattegno, en muchos países de todo el mundo.
En el sistema, hay 10 regletas de 1 cm a 10 cm. A las regletas de igual longitud se les asigna el mismo color.
Las regletas de Cuisenaire siguen este sistema:
Regleta Blanca = 1 cm.
Regleta Roja = 2 cm.
Regleta Verde claro = 3 cm.
Regleta Carmín = 4 cm.
Regleta Amarilla = 5 cm.
Regleta Verde Oscuro = 6 cm.
Regleta Negra = 7 cm.

Regleta Café = 8 cm.
Regleta Azul = 9 cm.
Regleta Naranja = 10 cm.

JCLIC

JClic es un entorno para la creación, realización y evaluación de actividades educativas multimedia, desarrollado en el lenguaje de programación Java

¿Qué es el JClic?

JClic está formado por un conjunto de aplicaciones informáticas que sirven para realizar diversos tipos de actividades educativas: rompecabezas, asociaciones, ejercicios de texto, palabras cruzadas ...

Las actividades no se acostumbran a presentar solas, sino empaquetadas en proyectos. Un proyecto está formado por un conjunto de actividades y una o más secuencias, que indican el orden en qué se han de mostrar.

El antecesor de JClic es Clic, una aplicación que desde 1992 ha sido utilizada por educadores y educadoras de diversos países como herramienta de creación de actividades didácticas para sus alumnos.

JClic está desarrollado en la plataforma Java, es un proyecto de código abierto y funciona en diversos entornos y sistemas operativos.

En las páginas de actividades de la zonaClic se ofrecen dos maneras de acceder a los proyectos JClic:

Visualizar las actividades en un applet

    Un applet es un objeto incrustado en una página web. Los proyectos que se ven de esta manera no quedan almacenados en el disco duro: JClic los descarga, los utiliza y finalmente los borra.

    Si el applet JClic no se pone en marcha correctamente hay que comprobar la configuración del sistema Java del ordenador. Se recomienda también echar un vistazo a la página en la que se explica el proceso de carga de los applets.

Instalar las actividades en el ordenador

    JClic tiene un asistente que permite descargar las actividades y guardarlas en la biblioteca de proyectos del ordenador. La biblioteca se crea la primera vez que se pone en marcha JClic, o cuando se intenta hacer la primera instalación de un proyecto.

    Para ver los proyectos de la biblioteca será necesario descargar e instalar JClic.

    Como en el caso anterior, si el instalador no se pone en marcha es probable que sea necesario comprobar la configuración del sistema Java del ordenador.

TABLA DE VERDAD

TABLA DE VERDAD

Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una
 proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes.

Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el
 que introdujo Ludwig Wittgensteinen su Tractatus logico-philosophicus, publicado en 1921

Las tablas nos manifiestan los posibles valores de verdad de cualquier proposición molecular, así como 
el análisis de la misma en función de las proposicíones que la integran, encontrándonos con los siguientes 
casos:

[editar]

Verdad Indeterminada o Contingencia

Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa,
 según los valores de las proposiciones que la integran. Sea el caso: .

Su tabla de verdad se construye de la siguiente manera:

Ocho filas que responden a los casos posibles que pueden darse según el valor Vo F de cada una de 
las proposiciones A, B, C. (Columnas 1, 2, 3)

Una columna (Columna 4) en la que se establecen los valores de  aplicando la definición del disyuntor 
a los valores de B y de C en cada una de las filas.(Columnas 2,3 → 4)

Una columna (columna 5) en la que se establecen los valores resultantes de aplicar la definición de la conjunción
 entre los valores de A (columna 1) y valores de la columna , (columna 4) que representarán los valores
 de la proposición completa , cuyo valor de verdad es V o F según la fila de los valores
 de A, B, y C que consideremos. (Columnas 1,4 → 5)

BLOQUES LÓGICOS

LOS BLOQUES LÓGICOS

Constan de 48 piezas sólidas, generalmente de madera o plástico, y de fácil manipulación. Cada pieza se define por cuatro variables: color, forma, tamaño y grosor. A su vez, a cada una de las piezas se le asignan diversos valores:
El color: rojo, azul y amarillo.

La forma: cuadrado, círculo, triángulo y rectángulo.

Tamaño: grande y pequeño.

Grosor: grueso y delgado.
Cada bloque se diferencia de los demás al menos en una de las características, en dos, en tres o en las cuatro.

Los bloques lógicos: utilidad-objetivos

Los bloques lógicos sirven para poner a los niños ante una serie de situaciones que les permitan llegar a adquirir determinados conceptos matemáticos y contribuir así al desarrollo de su pensamiento lógico.

A partir de la actividad con los bloques lógicos, el niño llegará a:
Nombrar y reconocer cada bloque

Reconocer cada una de sus variables y valores

Clasificarlos atendiendo a un solo criterio, como puede ser la forma o el tamaño, para pasar después a considerar varios criterios a la vez.

Comparar los bloques estableciendo las semejanzas y las diferencias.

Realizar seriaciones siguiendo distintas reglas.

Establecer la relación de pertenencia.

Definir elementos por la negación.
Los bloques lógicos son un gran recurso pedagógico en la etapa de Educación Infantil. Son infinitas las actividades que podemos llevar a cabo en el aula a través de los bloques lógicos, y por ello, mencionaré algunas de las actividades a las que mejor responden los niños desde mi experiencia docente.

1. Juego libre
Construcciones, de forma que se vayan familiarizando con ellos.

Dibujar la silueta sobre el papel.

Juegos de simulación: tenderos, mamás...

 aquí este mismo ejercicio le podemos llevar luego al papel.

MICROCOMPUTADOR DE PAPY

El Mini Computador Papy

Lo conversado en clases!  Les dejo un enlace que resume de modo "agradable" la existencia y utilización de este recurso, espero que les guste, es muy entretenido y a los niños les encanta (les aseguro que no tendrán problemas con aprender a utilizarlo)


Georges Papy (Nacido en 1920 en Bruselas) es un matemático belga. Profesor en la Universidad Libre de Bruselas y presidente de la Comisión Internacional para el Estudio y Mejoramiento de la Enseñanza de la Matemática, sus trabajos se han centrado sobre los problemas pedagógicos planteados por la matemática moderna. Entre sus obras destacan Iniciación a los espacios vectoriales y Matemática moderna.

Georges Papy se doctoró en matemática en la Universidad de Bruselas y pronto enseño allí y en otras universidades extranjeras. Consagrado a la reforma de la enseñanza de la matemática en la escuela secundaria, desde 1961 dirige el Centro Belga de Pedagogía de la Matemática. Si bien los temas expuestos en esta obra son de gran trascendencia en la matemática moderna, su mérito fundamental consiste en el uso de recursos pedagógicos novedosos que hacen más accesible la materia.

Se destaca el minicomputador de Papy (MIC) como sistema de representación y la conexión que hace entre este material didáctico y la comprensión por parte de los niños de las estructuras multiplicativas y aditivas. El minicomputador de Papy ha sido utilizado en el Colegio Refous de Bogotá, Colombia. Estos trabajos han sido dirigidos por Roland Jeangros con el apoyo del Grupo Nicosuba y compartidos por docentes de escuelas normales en los encuentros que organiza el colegio.

ALGEBRA DE CONJUNTOS

Álgebra de conjuntos
Artículo principal: Álgebra de conjuntos.
Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:
Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.

Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.

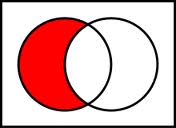
Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.

Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.
Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer (segundo) elemento pertenece a A (a B).